Recherche
- Électrons fortement corrélés, supraconductivité et matériaux quantiques.
- Problématique
- Objectifs
- Méthodologie
- Réalisations
- Collaborateurs
- English Summary
- Qubits supraconducteurs
- Projets étudiants
3. Méthodologie
Plusieurs méthodes analytiques ont été développées pour comprendre les systèmes fortement corrélés. Aux fonctions de Green des années 60 s'est ajouté le groupe de renormalisation dans les années 70, puis les méthodes de simulation numérique et les méthodes de type non-perturbatives (bosons esclaves et développements en 1/N) dans les années 80 et enfin des méthodes comme la théorie de champ moyen dynamique dans les années 90. Les méthodes numériques étaient d'abord assez limitées, mais grâce à des développements algorithmiques et à l'augmentation de la puissance de calcul des ordinateurs, il est maintenant possible de faire des simulations fiables dans des régimes de paramètres intéressants.
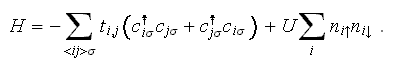
Hamiltonien du modèle de Hubbard
Le modèle dit de Hubbard tient compte de la façon la plus simple possible de la physique qui influence le comportement des électrons dans de tels systèmes, soit la présence d'un réseau cristallin et l'existence de répulsion entre lesdits électrons. Nos efforts se concentrent sur ce modèle avant d'attaquer des modèles plus complexes.
Nous utilisons plusieurs approches complémentaires. Du côté analytique, nous avons développé une nouvelle approche non-perturbative qui permet d'obtenir des résultats supérieurs à ceux des autres approches lorsqu'on les compare aux simulations Monte Carlo. Notre approche prédit des effets physiques nouveaux. Nous continuons de développer cette méthode en plus de l'appliquer à différents problèmes. Les simulations numériques sont aussi essentielles, entre autres pour nous permettre de tester la validité des méthodes analytiques puisque celles-ci sont en général approximatives. Nous avons développé des programmes de simulations numériques sophistiqués que nous mettons maintenant à profit pour réaliser nos objectifs. Il n'existe maintenant dans le monde qu'une dizaine de groupes qui ont développé cette expertise. Nous utilisons plusieurs ressources de calcul numérique. En plus des ordinateurs du Réseau Québécois de Calcul Haute Performance, à Sherbrooke Alain Veilleux, Michel Barrette et Mehdi Bozzo-Rey ont monté une grappe d'une soixantaine de processeurs Intel (classe Beowulf, voir image) qui nous permettent d'atteindre des vitesses de calcul comparables aux super-ordinateurs. Une subvention d'infrastructure obtenue de la Fondation Canadienne de l'Innovation et du programme de Chaires de Recherche du Canada nous permet maintenant de mettre au point une grappe de plus de 200 processeurs dont la première phase (100 processeurs) devrait être opérationnelle en 2002.

Elix1, la deuxième grappe Beowulf (linux) au Québec (et première à Sherbrooke, 1999). 64 processeurs Intel.
 |
 |
 |
| 2. Objectifs | Recherche | 4. Réalisations |